概率思维的重要性
- 概率思维是探索未知和不可控事物的数学工具。
- 概率思维的核心并不是教你如何在少量的信息获得决策,而是要让你知晓信息的重要性。
- 概率思维本质上是通过运用一些数学和逻辑工具,估算特定结果出现的可能性。
- 概率思维可以帮助我们确定最有可能出现的结果,从而更精确、有效地做出决策。
概率思维的组成部分
- 贝叶斯统计(也可以称为贝叶斯更新):贝叶斯是英国18世纪上半叶的一名牧师,其最知名的作品《机会学说中一个问题的解》(An Essay Toward Solving a Problem in the Doctrine of Chances)由他的朋友理查德·普莱斯于1763年(贝叶斯死后两年)带入英国皇家学会的视野。这篇文章关注的是当我们遇到新的数据时,我们应该如何调整概率。这篇文章为伟大的数学家皮埃尔·西蒙·拉普拉斯(Pierre Simon Laplace)推动贝叶斯定理的发展奠定了基础。鉴于我们对这个世界的了解比较有限,但了解到的信息都十分有用,而且会不断遇到新的信息,我们或许应该在学习新知识的同时认真考虑已知的内容,越多越好。贝叶斯思维告诉我们,概率是动态的,具有主观性。大多数决策都是“不完全信息决策”,而在不完全信息情况下,只靠聪明才智或努力也不一定有正确的决策。不要着急下结论,而是尽可能的收集相关的信息,识别出关键因素,提高决策成功的概率。(举个例子,不同事情的成功率对不同的人来说成功率是不同的。因为每个人的个人本身条件不同包括经验,各方信息,对客观情况的了解情况,分析能力等等,成功率是不一样的。不要把概率当成一个不变的值,概率会因为条件不同而有了不同的数值),不要急于下决定,尽可能的获取相关的条件信息再考虑。只有做了这些工作和思考,你才能知道哪条路才是最适合自己的。在信息缺失的环境下盲目下结论,只是一种赌博。
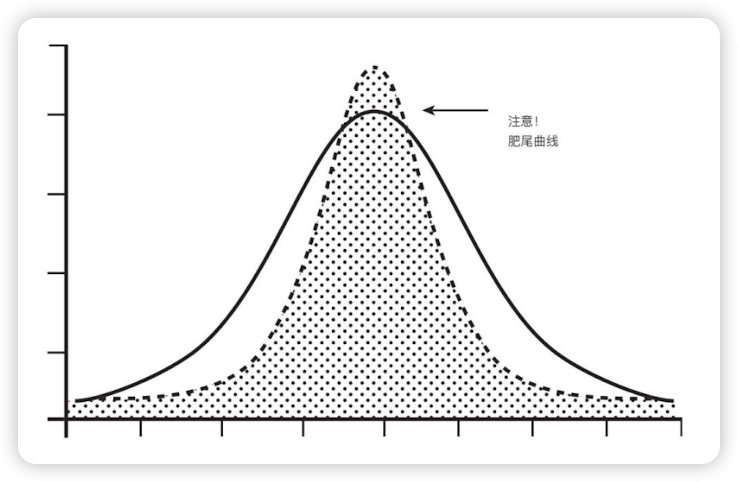
- 肥尾曲线:肥尾理论告诉我们坏事总会发生,只是不知道什么时间而已。坏事情发生的概率往往高于预期,在这里要做的并不是坐在原地然后考虑各种肥尾的情况发生,有时候放弃一些利益换取更为稳定的方式可能会避免更大的损失。(钟型分布曲线的极限值通常是有限的,可计算的;但是肥尾曲线的影响暂时来说是无法计算的。钟型分布曲线的极限值通常是有限的,可计算的;但是肥尾曲线的影响暂时来说是无法计算的。)
- 非对称:指的是“乐观”统计的概率通常大于“悲观”统计的概率,换句话说,成功的概率总是高于失败的概率。
- 稀缺思维:由事物稀缺形成的一种稀缺心态,而这个过程是无意识的。人习惯性地专注于解决目前稀缺状况,导致错过更重要的选择和时机。
- 我们总会高估成功率而低估失败率。在估算事物价值的时候要注意稀缺思维,因为稀缺而错估价值的情况经常会无意识的发生。经常复盘能够减少这种情况的发生。
概率思维的应用
- 反脆弱思维:纳西姆·塔勒布在《反脆弱》中提出核心观点,事物分为三种类型:受到波动性和不可预测性负面影响的、面对波动性和不可预测性不受任何影响的,以及受益于波动性和不可预测性的。最后一类便属于反脆弱状态,在某种程度上,某些事物会从波动中受益,也应该成为我们的目标。为什么呢?因为这个世界从根本上来说就是变化多端、不可预测的,大事件(恐慌、崩溃、战争、泡沫等等)往往会对结果产生巨大的影响。反脆弱和概率思维之间的关系在于,一个具有反脆弱特性的系统或个体,需要了解自身面对各种风险和不确定性的应对能力,这需要运用概率思维来预测并准备未来可能的冲击。同时,通过概率思维,我们能够理解和接受事物不确定的本质,这也是培养反脆弱性的重要一步。做好准备,用反脆弱性武装自己,进而从世界的动荡中受益。
- 如何反脆弱收益呢?一是寻找我们认为存在更多机会的情况;二是学习如何“正确地”失败。适度冒险,避免跌倒了一次就一蹶不振(永远不要彻底离场);其次,培养韧性,从失败中学习,然后东山再起。失败赋予了我们反脆弱的能力——学习。
- 间谍思维:成功的间谍非常擅长概率思维,他们必须尽可能不带偏见地评估自己所处的环境。(比如二战期间英国特别行动处的薇拉·阿特金斯通过概率思维,大大的扰乱了德国在法国的行动)
- 全世界对概率最具敏感性的公司当属保险公司,因为它们必须注重概率。
- 伟大的保险公司都知道如何关注重要的因素,哪怕它们不是完全可预测的,并相应地进行定价。
《反脆弱》的心态非常独特。只要有可能,试着让随机性和不确定性成为你的朋友,而不是你的敌人。
结论
高效的概率思维意味着你首先要大致确定什么是最重要的因素,估计自己有几分胜算,验证假设,然后做出决定。在不可预测的复杂情况下,我们可以更有把握地采取行动。我们永远无法精确地预知未来。概率思维是一种非常有用的工具,可以用来评估未来可能的世界面貌,以便我们有效地制定战略。